4.10 Definición de diferencial.

Definición de diferencial

Eun diferencial se refiere a un cambio infinitesimal en una variable y a la forma en que afecta a una función. Es un concepto central en el cálculo diferencial y puede entenderse desde dos perspectivas:

1. Geometría y cálculo diferencial:
   El diferencial de una función $f(x)$ en un punto $x$ representa la aproximación lineal del cambio en $f(x)$ debido a un cambio pequeño en $x$. Matemáticamente, se define como:

   $$dy = f'(x) \, dx$$

   Donde:

   • $dx$ es un cambio infinitesimal en la variable $x$.
   • $dy$ es el cambio correspondiente en $y = f(x)$ basado en la pendiente $f'(x)$, que es la derivada de $f(x)$.

2. Interpretación práctica:
   En términos simples, el diferencial proporciona una herramienta para analizar cómo una pequeña variación en la entrada de una función afecta su salida. Esto es útil en aplicaciones como física, ingeniería y economía para aproximar valores y entender relaciones entre variables.

El concepto de diferencial es clave en múltiples áreas, como la optimización, el análisis de errores y la resolución de problemas relacionados con tasas de cambio.

Consideremos la siguiente ilustración en donde aproximamos a la función f por su recta tangente.

 

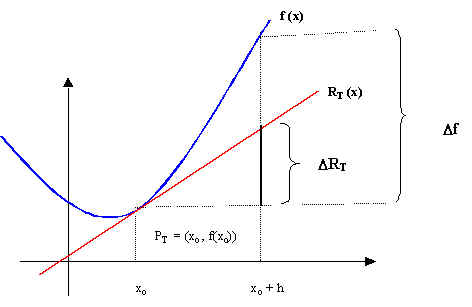
Considerando que la recta tangente es la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia P_T, si le llamamos  a la variación de f cuando x varía de x_o a x_o + h y  a la variación de la recta tangente en el mismo rango de variación en x, podemos afirmar que para valores de h "cercanos" a 0, estas dos variaciones son muy parecidas, es decir, D f @ D R_T .

Podemos expresar a D R_T en términos de h y el ángulo q que forma la recta tangente con el eje de las abscisas. En el triángulo de la figura, que extraemos a continuación, se observa lo siguiente:

 

 

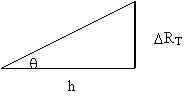
En virtud de que D R_T es un aproximador de la DIFERENCIA D f, lo definiremos como EL DIFERENCIAL DE f en el punto x_o, con respecto al incremento h y lo denotaremos por df, es decir,

df = f '(x_o)h

Observación: El diferencial, en general depende de h y del punto x_o. Por ejemplo el diferencial de f(x) = x² es:

df = f ' (x_o)h = (2x_o)h

que también lo podemos expresar como:

d(x²) = (2x_o)h

Si especificamos el punto x_o, el diferencial dependerá únicamente de h, como se aprecia en los siguientes ejemplos:

 

a) El diferencial de f(x) = x² en x_o =3 es d(x²) = 6h

b) El diferencial de f(x) = x² en x_o =7 es d(x²) = 14h

c) El diferencial de f(x) = x³ en x_o =2 es d(x³) = 12h

En el caso de la función identidad f(x) = x, como f '(x_o) = 1 para todo x_o, su diferencial nos queda como df = f '(x_o)h = h o bien dx = h

Como h es el diferencial de la función identidad, podemos re-escribir el diferencial de una función f derivable en x_o, como:

df = f '(x_o)dx

Esta expresión nos dice que la variación de una función f es aproximadamente proporcional a la variación de su variable independiente, donde la constante de proporcionalidad es la derivada en el punto en cuestión.

En los siguientes ejemplos estimaremos la variación D f para x_o y h dados y la compararemos con el diferencial.

Ejemplo . Verifique que:

a) Para f(x) = x² se cumple que D f @ df en x_o = 1 y h = 0.1

      Solución:

D f = f(1.1) - f(1) = 1.21 - 1 = 0.21

df = f ' (1)dx =(2x|_x=1 )(0.1) = (2)(0.1) = 0.20

La variación real difiere de la aproximada en una centésima.

Observación: El punto x_o + h es un punto cercano a x_o, que se encuentra a la derecha de éste si h es positivo y a la izquierda si h es negativo. En el siguiente ejemplo consideraremos un incremento negativo.