4.9 Problemas de Optimización.

 

Problemas de Optimización

El hombre siempre se enfrenta con el problema de encontrar la mejor manera de obtener la ganancia, al menor costo. Por ejemplo, el ranchero quiere escoger la mezcla de pastos para poder obtener el mayor aprovechamiento, un científico desea escoger y aplicar la menor dosis de una vacuna para obtener el mayor aprovechamiento, un fabricante desea minimizar el costo de producción de un producto. Algunas veces, problemas que se presentan ante la vida real, pueden formularse y resolverse, al involucrar una función y así es como el cálculo se vuelve una herramienta muy poderosa para poder resolver este tipo de cuestionamientos.

La invención de Isaac Newton se vio lograda, en un momento de encierro, ya que, en 1665, la gran plaga de la peste hizo que se fuera a un retiro en su casa de casi 18 meses y ahí en retiro surgió su método de fluxiones (lo que conocemos hoy como el cálculo diferencial).

El criterio de la primera derivada proporciona la monotonía de una función $f$ derivable en un intervalo $I=(a,b)$:

• $f$ es creciente en $I$ si $f^{\prime }\left(x\right)>0$ para todo $x\in I$
• $f$ es decreciente en $I$ si $f^{\prime }\left(x\right)<0$ para todo $x\in I$

Como consecuencia, los puntos que anulan la primera derivada (llamados puntos críticos) son candidatos a ser extremos relativos.

Por tanto, para resolver los problemas tenemos que

1. Platear la función $f\left(x\right)$
2. Calcular la derivada $f^{\prime }\left(x\right)$
3. Calcular los puntos críticos (soluciones de $f^{\prime }\left(x\right)=0$)
4. Determinar si los puntos críticos son máximos o mínimos a partir de la monotonía

También, se puede aplicar el criterio de la segunda derivada para el paso 4.

Ejemplo

El coste de fabricación de una bolsa hermética de plástico viene dado por la función

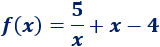
siendo $x>0$ el volumen de la bolsa (en litros).

¿Cuál debe ser el volumen de la bolsa para que su coste sea mínimo? ¿Cuál es dicho coste?

Derivamos la función:

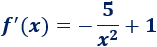
Igualamos la derivada a $0$ y resolvemos:

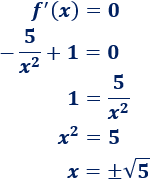
El único punto crítico que tenemos es $x=\sqrt{5}$ (descartamos el negativo porque $x$ debe ser positiva).

El signo de la derivada se mantiene constante en los intervalos

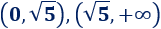
Evaluamos la derivada en cualquier punto de cada intervalo:

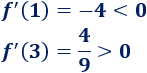
Por tanto, la función es decreciente el primer intervalo y creciente en el segundo. Esto implica que el punto crítico es un mínimo de la función.

El volumen debe ser $\sqrt{5}$ litros para que el coste sea mínimo.

Calculamos el coste:

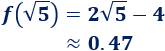
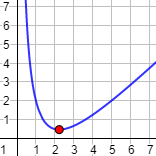
Gráfica de la función (para $x>0$):